Уметь быстро сосчитать в уме разницу или сумму двух- или даже трехзначных чисел — важный навык, который не только поможет быстро справиться с контрольной и впечатлить учителя, но и сделает математику понятнее и интереснее.
Часто дети плохо считают в уме. В некоторых программах детей во 2-м классе учат считать в столбик, и они начинают все вычисления делать на бумаге. Или же ребята выучивают самый популярный способ счёта «десятки отдельно, единицы отдельно» и применяют его во всех случаях.
Например, 45 + 19 считают как 40 + 10 + 5 + 9 = 50 + 14 = 64. Так тоже можно, но это не всегда удобно и быстро. Вместо этого можно вычислить 45 + 20 — 1 = 65 — 1 = 64.
Такие хитрые приёмы счёта мы тренируем на кружке почти на каждом занятии: после этого наши ученики становятся увереннее на школьных уроках и меньше ошибаются в решениях. В этой статье расскажем о приемах на сложение и вычитание. Вы можете потренировать их со своими детьми: они работают на разных числах, так что неважно, в 1-м классе у вас ребенок или в 4-м.
1. Переместительное и сочетательное свойства
Это самые базовые приёмы. Их изучают в школе, но мы дополнительно их тренируем: ребенку важно научиться видеть числа, удобные для сложения, а не складывать всё подряд.

2. Прибавление почти круглого числа
Прибавлять «круглые» числа, то есть, целые десятки, сотни и так далее, всегда удобно. Поэтому, если слагаемое близко к круглому, можно представить его в виде разницы этого круглого числа и «лишних» единиц:
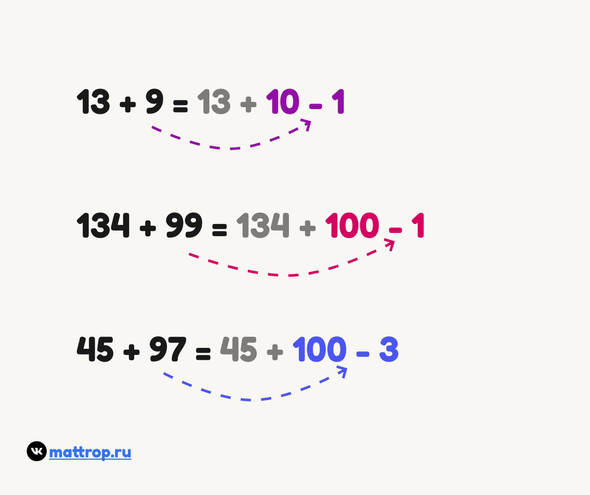
35 + 6 = 35 + 10 — 4 — так сделать тоже можно, но это уже не очень удобно. Способ хорошо работает с числами, оканчивающимися на цифры больше шести: 7,8 и 9. Здесь и в других приемах важно, чтобы ребёнок уже хорошо знал состав числа 10. И понимал сколько нужно прибавить к числу, чтобы сумма стала равна десяти.
3. Вычитание почти круглого числа
Здесь идея такая же, как и в предыдущем приёме: вычесть круглое число удобнее, поэтому можем представить вычитаемое в виде разницы круглого числа и «лишних» единиц:
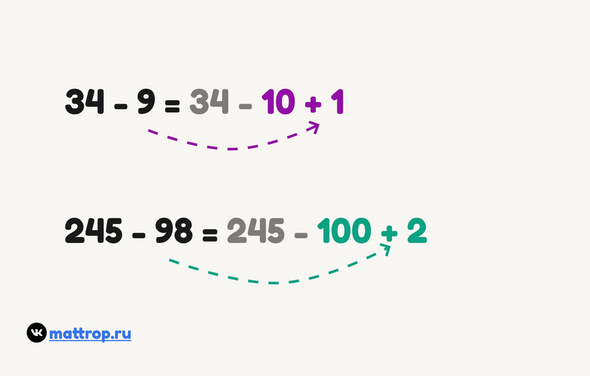
Будьте внимательны при тренировке этого приёма: дети иногда ошибаются в нём и применяют его так: 45 — 18 = 45 — 20 — 2 = x, а надо: 45 — 18 = 45 — 20 + 2 = x. Чтобы избежать ошибки, проговаривайте действия: мы должны были вычесть 18, но забираем у 45 20, а это больше на 2 единицы. Значит, двойку мы должны «вернуть», то есть, прибавить 2.
4. Разложение на удобные слагаемые (сложение)
Суть приёма в том, что пример из одного действия мы разбиваем на два действия, которые легко выполнить. Этот способ с трудом даётся детям поначалу, но после освоения на практике хорошо помогает при счёте.

5. Разложение на удобные слагаемые (вычитание)
Здесь мы применяем такую же идею, как и в предыдущем приёме — ищем, как можно разложить число, которое вычитаем, чтобы было удобнее вычислять.
Такой приём хорошо подходит в том случае, если единицы уменьшаемого меньше, чем вычитаемого.
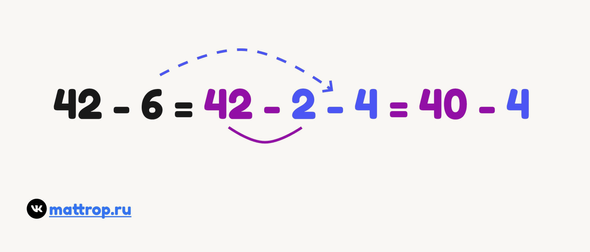
6. Вычитание с помощью сложения
Этот способ необычный и поначалу сложный для понимания, но после освоения позволяет легко вычитать даже большие числа без калькулятора.
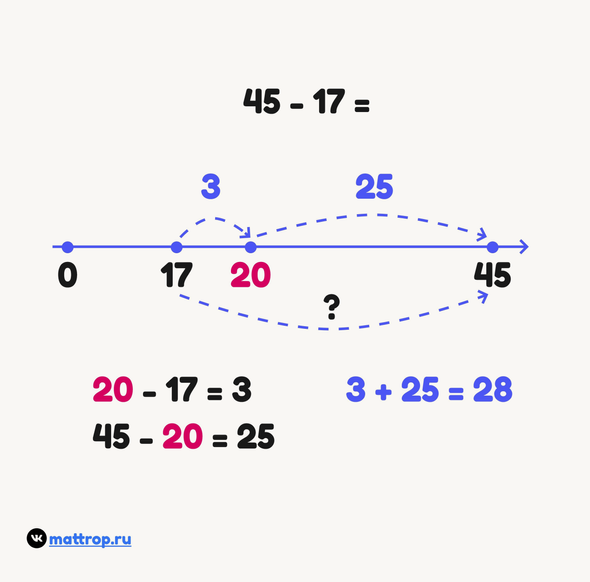
Посмотрим на примере: 45 — 17 =
Первое, что нужно понять, что вычитание — это поиск расстояния между числами 17 и 45 на числовой прямой.
Выберем на прямой круглое число между 17 и 45, до которого нам удобнее считать расстояние. Пусть это будет 20.
от 17 до 20 расстояние 3
от 20 до 45 расстояние 25
Значит, общее расстояние: 25 + 3 = 28
Попрактикуемся? Даже такой «страшный» пример можно легко посчитать с помощью этого способа: 317 — 129 =
Между 371 и 129 выберем круглое число — 200.
от 129 до 200 расстояние 71.
от 200 до 317 расстояние 117.
117 + 71 = 188.
Мы могли бы выбрать в качестве числа «посередине» 300. Какими именно промежутками считать — не так важно, главное — чтобы было удобно вычислять.
Понимание этих приёмов помогает автоматизировать устный счёт. Совсем не обязательно потом применять их все — каждый выбирает себе то, что удобнее и лучше запомнилось.





